Realiza e interpreta paso a paso un ANOVA de medidas repetidas en R-Software.

Contenidos

• ¿Qué es el ANOVA MR?
• ¿Por qué utilizar pruebas específicas para muestras relacionadas?
• El modelo más simple
• Ejemplo de un experimento de un factor con medidas repetidas
• ¿Qué datos utilizaremos?
• Manipulación de los datos, descriptivos y supuestos
• Pruebas de hipótesis
• Introducción al ANOVA mixto de 2 factores

¿Qué es el ANOVA MR?

Los modelos de análisis de varianza (ANOVA) con medidas repetidas (MR) sirven para estudiar el efecto de uno o más factores cuando al menos uno de ellos es un factor intra-sujetos.

Hablamos de medidas repetidas cuando el mismo sujeto o caso participa de todas las condiciones de un experimento o cuando se tiene de ellos múltiples valores en el tiempo.

La diferencia entre el ANOVA clásico que ya hemos visto en este blog (¿Cómo realizar el ANOVA de una vía en R?) y el ANOVA de medidas repetidas que hoy veremos es que el primero trabaja con muestras independientes y el último con muestras relacionadas.

¿Recuerdas la diferencia entre muestras independientes y muestras relacionadas? Si quieres refrescar tu memoria visita nuestro post GUÍA DEFINITIVA PARA ENCONTRAR LA PRUEBA ESTADÍSTICA QUE BUSCAS.

ÚLTIMAS PLAZAS EN MASTERS

Máster Data Science

CONVOCATORIA ABIERTA I Logra la máxima precisión y rigor en tus proyectos de Ciencia de Datos.

Ver convocatorias 2022

MAster en MAchine learning

CONVOCATORIA ABIERTA | Automatiza procesos y crea tus propios algoritmos de Machine Learning.

Ver convocatorias 2022

¿Por qué utilizar pruebas específicas para muestras relacionadas?

Y te preguntarás ¿por qué tanto jaleo? ¿por qué es necesario tener en cuenta si las muestras son independientes (sobre sujetos o elementos distintos) o relacionadas (tomadas sobre los mismos sujetos o elementos)?

• Si las muestras están relacionadas, entonces los valores de una muestra afectan los valores de la otra muestra. Por ejemplo, si realizamos varias medidas de la tensión arterial a un grupo de sujetos, un sujeto que es hipertenso y tiene un valor alto en la primer muestra es de esperar que también tenga una tensión alta en la segunda o tercer muestra. Y esto debes tenerlo en cuenta en el error de tus análisis.
• Además, los diseños de medidas repetidas requieren menos sujetos que un diseño de muestras independientes y permiten eliminar la variación residual debida a las diferencias entre los sujetos (pues se utilizan los mismos).

Sin embargo, tendremos que tener en cuenta problemas tales como el efecto de arrastre, el efecto del aprendizaje por la práctica, etc., debido justamente a utilizar los mismos individuos en el experimento.

El modelo más simple

El ANOVA MR nos permite evaluar de manera global si para nuestra variable respuesta las medias de K poblaciones (K>2) son iguales (hipótesis nula) o si al menos una de ellas no es igual al resto (hipótesis alternativa).

En el caso de que rechacemos la hipótesis nula nos puede interesar saber exactamente entre qué poblaciones existen diferencias significativas; para ello utilizaremos comparaciones múltiples post hoc y los estadísticos descriptivos para interpretar los resultados.

Supuestos

I. Normalidad. Los errores del modelo siguen una distribución normal.

Este supuesto lo vamos a comprobar mediante la prueba de normalidad de Shapiro-Wilks.

II. Valores atípicos (outliers).

Utilizaremos un gráfico de cajas de la variable respuesta por muestra que queremos comparar, para evaluar este requisito.

III. Esfericidad.

En el ANOVA clásico inter-sujetos hemos visto que debe cumplirse el supuesto de que todas las puntuaciones de diferentes condiciones sean independientes. Cuando tenemos medidas repetidas no podemos cumplir con este supuesto ya que las mediciones están relacionadas porque provienen de un mismo sujeto. Por lo tanto, debemos “cambiar” este supuesto por otro válido.

Asumiremos que la relación entre pares de condiciones experimentales es similar, es decir, que el nivel de dependencia entre las condiciones experimentales es igual. A este supuesto le llamamos esfericidad o circularidad, y es un concepto relacionado con el supuesto de homogeneidad de varianza del ANOVA clásico inter-sujetos. La esfericidad implica la igualdad de varianzas de las diferencias ente niveles de tratamiento. Este supuesto lo vamos a comprobar mediante la prueba de Mauchly cuya hipótesis nula implica que las varianzas de las diferencias entre condiciones son iguales

Si la prueba es significativa (p<0.05) concluimos que existen diferencias significativas entre las varianzas de las diferencias y que por lo tanto la condición de esfericidad no se cumple y podemos optar por dos soluciones alternativas.

Bien podemos basar nuestra decisión en los estadísticos multivariados (a los que no les afecta el incumplimiento del supuesto de esfericidad) o podemos utilizar el estadístico F univariado aplicando un índice corrector llamado épsilon (Box, 1954). Podemos utilizar el epsilon de Greenhouse-Geisser (GG; 1959; Geisser y Greenhouse, 1958) o el de Huynh-Feldt (HF; 1976), siendo la primera de ellas algo más conservadora. Con este índice corrector podemos corregir los grados de libertad de F (tanto los del numerador como los del denominador) para satisfacer los requerimientos estadísticos de la prueba.

Si no se incumple el supuesto de esfericidad es preferible utilizar la aproximación univariada.

Ejemplo de un experimento de un factor con medidas repetidas

¿Qué datos utilizaremos?

Vamos a estudiar una única variable en distintos momentos temporales.

Vamos a utilizar los datos “hangover” del paquete WRS2, donde vamos a evaluar cómo transcurren los síntomas de la resaca después de consumir igual cantidad de alcohol. Las mediciones del número de síntomas de la resaca se realizaron en tres ocasiones la mañana siguiente a consumir alcohol (muestras relacionadas).

Nos preguntamos, sin diferenciar por grupo experimental, ¿los sujetos disminuyen su grado de resaca con el tiempo? ¿en qué momento? ¿en la segunda o en la tercera medición?

Queremos es comparar el número de síntomas de resaca en 3 tiempos de medición distintos (muestras relacionadas).

1. Manipulación de los datos, descripción y supuestos

Procedimiento

• obtener los datos
• realizar un análisis descriptivo de los datos.

* comprobación de los supuestos (normalidad y presencia de outliers).

Debemos primero instalar la librería WRS2 (si es que aún no la tienen instalada) para acceder a los datos.

Puedes descargar el paquete desde el repositorio CRAN de R con:

install.packages(“WRS2”)

O descargarlo desde GitHub así:

library(devtools)

install_github(“cran/WRS2”)

Ahora solo queda activar la librería y los datos:

Vemos que tenemos 4 variables:

• symptoms: Número de síntomas de la resaca
• group: Hijo de alcohólico vs. control
• time: Momento de la medición
• ID: identificación del sujeto

Aquí no utilizaremos la variable “group” que diferencia entre hijos de padres alcohólicos y los que no, pero podríamos incluir este factor de grupo, y su posible interacción con el tiempo de medición, utilizando un ANOVA mixto (lo dejo para vosotros).

Una vez tenemos los datos, vamos a realizar un análisis descriptivo para tener una idea de cómo son nuestros datos y luego analizamos los supuestos de la prueba (i.e. normalidad y ausencia de valores atípicos -outliers-).

Descriptivos y análisis de outliers.

Vemos que tenemos 40 casos (o sujetos) para cada una de las 3 muestras de tiempo.

Realizamos ahora un resumen numérico para cada muestra y el gráfico de cajas (boxplot):

Vemos que no varía demasiado el número de síntomas en las 3 mediciones, aunque el tiempo 1 parece tener menor número existe mucha dispersión en los datos. También observamos la presencia de datos atípicos (outliers; los puntos del gráfico) que podrían indicarnos que es mejor realizar pruebas robustas para el ANOVA MR.

Ahora comprobamos el supuesto de normalidad.

Prueba de normalidad de Shapiro-Wilks

En los 3 tiempos la variable “symptoms” no tiene distribución normal, sería interesante desarrollar pruebas no paramétricas que no trabajan bien para datos que no son normales.

También podríamos realizar un gráfico Q-Q para evaluar este supuesto (lo dejo en vuestras manos!).

> NOTA: Aunque en este post no veremos la versión del ANOVA MR no paramédico ni el robusto, puedes consultar nuestro POST “Guía definitiva para encontrar la prueba estadística que buscas” para ver qué función en R puedes utilizar para ello.

Interpretación

Según el gráfico de cajas y los estadísticos descriptivos, el número de síntomas de resaca no parece variar demasiado en el tiempo, aunque la respuesta se vuelve más variable.

Las pruebas de normalidad indican falta de normalidad debido a la gran presencia de ceros y hemos detectado datos atípicos (u outliers)

2. Pruebas de hipótesis

A. ¿Existen diferencias entre los tiempos?

Tenemos una variable dependiente numérica (symptoms) y la queremos comparar entre 3 niveles de una variable categórica (time) que corresponden a muestras relacionadas porque son observaciones de los mismos sujetos. Debemos utilizar un ANOVA de 1 vía o 1 factor intra-grupos o de medidas repetidas.

Para el caso del ANOVA de 1 factor intra grupos, las hipótesis que corresponden son:

• H0: el número de síntomas de resaca es el mismo en los 3 tiempos (los sujetos, independientemente de si son hijos o no de padres alcohólicos, no variaron su nivel de resaca en el experimento).
• H1: en algún momento el grado de resaca cambió (existen diferencias entre al menos alguno de los 3 tiempos de medición

B. ¿Entre qué tiempos específicamente?

Luego de evaluar si existen diferencias entre los 3 tiempos de medición, y si obtenemos un resultado significativo (si hay diferencias), nos interesará evaluar entre qué tiempos específicamente encontramos estas diferencias. Para ello utilizaremos las comparaciones múltiples post hoc.

Procedimiento

• Realizar la prueba ANOVA MR paramétrica con ezANOVA()
• Realizar comparaciones múltiples post hoc con t.test()

> NOTA: la prueba ezANOVA necesita que los datos estén en formato long, es decir, la variable de medidas repetidas tiene que estar dada en una única columna (como en este caso). Si los datos no tuvieran esta estructura se debe pasar de formato wide a long como se especificó en el tema 1.

Para realizar el ANOVA MR debemos ingresar los datos en la función ezANOVA() indicando los datos (data), la variable dependiente o respuesta (dv), la identificación de los sujetos (wid), y la variable de tiempo (within).

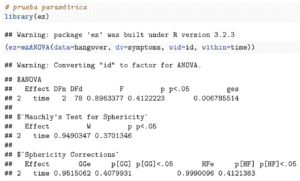
En este caso la prueba de esfericidad de Mauchly no es significativa (ver $Mauchly’s test for sphericity), por lo cual no rechazamos el supuesto de esfericidad y no tendremos que utilizar una corrección para la esfericidad ($Sphericity correction), nos basta con mirar el resultado del estadístico F univariado ($ANOVA).

No hay diferencias significativas en los 3 tiempos (F(2,78)=0.89, p=0.41), es decir, el número de síntomas de resaca no difiere significativamente entre los 3 tiempos de medición.

El ejercicio debería terminar aquí, pero por motivos didácticos vamos a realizar las pruebas de comparaciones múltiples post hoc que nos permitirían evaluar entre qué grupos hay diferencias significativas en el caso de que la prueba de ANOVA MR anterior hubiera sido significativa:

Los resultados coinciden con el ANOVA MR anterior, vemos que los 3 p-valores que nos muestra esta prueba no son significativos. Por ejemplo, la prueba que compara el tiempo 1 vs tiempo 2 presenta un p-valor de 0.26, tiempo 1 vs tiempo 3 tiene un p=0.24 y tiempo 2 vs tiempo 3 p=0.86.

> NOTA: podrías utilizar la corrección de Bonferroni para estas comparaciones, consúltalo en la ayuda de la función ?pairwise.t.test

Interpretación

La prueba ANOVA MR paramétrico no indica diferencias significativas, pero recordemos que nuestras variables no son normales y presentan outliers, así que estos resultados no son fiables.

Introducción al ANOVA mixto de 2 factores

Imagina que ahora queremos responder a la siguiente pregunta: Los hijos de padres alcohólicos y los de padres no alcohólicos, ¿se comportan de la misma manera? o ¿cuál de ellos se recupera antes de la resaca?

Este tipo de preguntas implica considerar 2 factores (group -entre grupos- y time -intra grupo o de medidas repetidas-) a la vez. Este tipo de problemas se resuelve mediante el ANOVA de 2 factores mixto.

Espero que este post te haya sido de gran ayuda y lo apliques pronto a tus propios datos.

Déjanos tu mensaje y cuéntanos tu experiencia.