¿Por qué la correlación no implica causalidad?

Definición, Diferencias y Ejemplos

Seguramente ya has escuchado hablar de que es importante no confundir la correlación con la causalidad.

En este post veremos varios ejemplos para comprender por qué un valor alto del coeficiente de correlación no indica causalidad, cómo puede influir una tercera variable generando una relación espuria y la paradoja de Simpson.

Finalmente veremos cómo utilizar la correlación parcial para evaluar si estamos ante una relación espuria debido a la presencia de una tercera variable de confusión.

Si la correlación no implica causalidad, entonces, ¿qué hace?

La correlación implica asociación, pero no causalidad.

A la inversa, la causalidad implica asociación, pero no correlación.

ÚLTIMAS PLAZAS EN MASTERS

Máster Data Science

CONVOCATORIA ABIERTA I Logra la máxima precisión y rigor en tus proyectos de Ciencia de Datos.

Ver convocatorias 2022

MAster en MAchine learning

CONVOCATORIA ABIERTA | Automatiza procesos y crea tus propios algoritmos de Machine Learning.

Ver convocatorias 2022

Ejemplos que demuestran que la correlación no es causalidad

Veamos algunos ejemplos para comprender esta precaución.

• La presencia de una correlación no siempre significa que haya una relación causal.

Por ejemplo, un estudio de 1999 publicado en Nature mostró que los niños menores de dos años que dormían con luces nocturnas tenían más probabilidades de tener miopía. Más tarde, otros investigadores demostraron que los padres miopes tenían más probabilidades de mantener sus luces encendidas por la noche. Puede ser que los padres fueran una causa común del uso de luces nocturnas y, en virtud de la herencia genética, la miopía se transmitió a sus hijos.

• La presencia de una relación causal no siempre significa que existe una correlación.

Supongamos que un termostato mantiene un hogar a una temperatura constante controlando un horno de aceite. Dependiendo de la temperatura exterior, se quemará más o menos aceite. Pero como el termostato mantiene la temperatura interior constante, la temperatura interior no tendrá correlación con la cantidad de aceite quemado. El aceite es lo que mantiene la casa caliente, una relación causal, pero no está correlacionada con la temperatura de la casa.

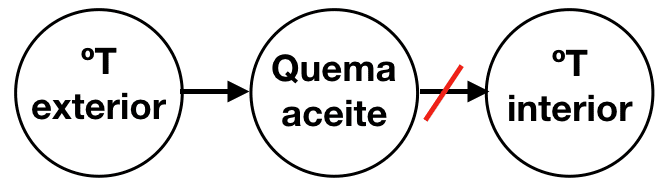
• Incluso si existe una relación causal entre dos variables, la correlación por sí misma no nos dice nada sobre la dirección de la causalidad.

Por ejemplo, se ha afirmado que los estilos de vida activos pueden proteger el funcionamiento cognitivo de las personas mayores. Pero algunas evidencias sugieren que la dirección causal es la opuesta: un funcionamiento cognitivo más alto puede resultar en un estilo de vida más activo.

También podemos encontrarnos con otro tipo de problemas.

• Puede existir una tercer variable medida o no medida que afecte los resultados de la correlación.

Por ejemplo, Hyndman & Athanasopoulos 2018 han visto que existe una relación entre el número mensual de ahogamientos en una playa con la cantidad de helados vendidos en el mismo período. Los helados no causan el ahogamiento, ni a la inversa, sino que las personas comen más helados en los días calurosos cuando también es más probable que vayan a nadar. Entonces, las dos variables (ventas de helados y ahogamientos) están correlacionadas, pero una no está causando la otra sino que ambas son causados por una tercera variable, la temperatura.

La relación entre la venta de helados y el número de ahogamientos es espuria.

Por último, la Paradoja de Simpson muestra que en determinados casos se produce un cambio en la relación entre un par de variables, cuando se controla el efecto de una tercera variable.

Por ejemplo, la asociación entre dos variables se puede invertir según cómo se agrupen los datos en subpoblaciones. La siguiente figura nos permite explicar la paradoja.

Imagina un experimento donde se evalúa la respuesta a un tratamiento farmacológico. Los datos en su conjunto indican que a mayor dosis del medicamento, mayor respuesta en los sujetos tratados (la línea negra). Sin embargo, cuando se dividen los resultados por género vemos que la relación es distinta según el sexo de los sujetos analizados.

Esto se debe a que en el experimento las mujeres tomaron los medicamentos con dosis más bajas y se observó que respondían menos al tratamiento (línea roja) en comparación con los hombres (línea azul). Es decir, el factor género confunde la relación entre dosis y respuesta.

Aquí, los resultados globales no permiten observar la estructura verdadera de los datos y conducen a conclusiones falsas, la relación dosis-respuesta en la población de interés es más compleja. Para evitar este tipo de problemas se puede utilizar análisis de estratificación donde se divide el análisis en estratos o grupos de interés (e.g. según el género de los sujetos).

Espero que estos ejemplos sirvan para recordar que:

CORRELACIÓN no implica CAUSALIDAD

Y tú, ¿qué opinas? Déjanos tu comentario y comparte qué herramientas utilizas para analizar correlaciones evitando encontrar relaciones espurias.