¿Qué es la correlación estadística y cómo interpretarla?

El análisis de correlación es el primer paso para construir modelos explicativos y predictivos más complejos.

A menudo nos interesa observar y medir la relación entre 2 variables numéricas mediante el análisis de correlación. Se trata de una de las técnicas más habituales en análisis de datos y el primer paso necesario antes de construir cualquier modelo explicativo o predictivo más complejo.

• Qué es la correlación
• Cómo se interpreta la correlación
• Cómo se mide la correlación
• Para qué sirve: ejemplos prácticos de correlación

¿Qué es la correlación

La correlación es un tipo de asociación entre dos variables numéricas, específicamente evalúa la tendencia (creciente o decreciente) en los datos.

Dos variables están asociadas cuando una variable nos da información acerca de la otra. Por el contrario, cuando no existe asociación, el aumento o disminución de una variable no nos dice nada sobre el comportamiento de la otra variable.

Dos variables se correlacionan cuando muestran una tendencia creciente o decreciente.

NOTA: Te recomiendo siempre comenzar a analizar la correlación realizando un diagrama de dispersión entre las variables que quieres analizar, te evitarás posibles problemas como el del ejemplo del cuarteto de Anscombe que les comenté en este post.

ÚLTIMAS PLAZAS EN MASTERS

Máster Data Science

CONVOCATORIA ABIERTA I Logra la máxima precisión y rigor en tus proyectos de Ciencia de Datos.

Ver convocatorias 2022

MAster en MAchine learning

CONVOCATORIA ABIERTA | Automatiza procesos y crea tus propios algoritmos de Machine Learning.

Ver convocatorias 2022

Cómo se interpreta la correlación

La correlación nos permite medir el signo y magnitud de la tendencia entre dos variables. En la figura 1 vemos diferentes valores del coeficiente de correlación y sus diagramas de dispersión correspondientes. Podemos ver que:

1. El signo nos indica la dirección de la relación, como hemos visto en el diagrama de dispersión.
   • un valor positivo indica una relación directa o positiva,
   • un valor negativo indica relación indirecta, inversa o negativa,
   • un valor nulo indica que no existe una tendencia entre ambas variables (puede ocurrir que no exista relación o que la relación sea más compleja que una tendencia, por ejemplo, una relación en forma de U).
2. La magnitud nos indica la fuerza de la relación, y toma valores entre -1 a 1. Cuanto más cercano sea el valor a los extremos del intervalo (1 o -1) más fuerte será la tendencia de las variables, o será menor la dispersión que existe en los puntos alrededor de dicha tendencia. Cuanto más cerca del cero esté el coeficiente de correlación, más débil será la tendencia, es decir, habrá más dispersión en la nube de puntos.
   • si la correlación vale 1 o -1 diremos que la correlación es “perfecta”,
   • si la correlación vale 0 diremos que las variables no están correlacionadas.

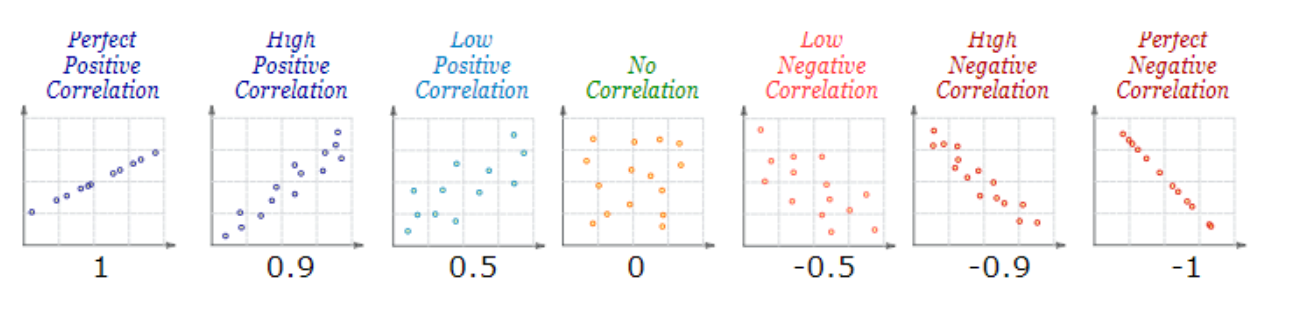
Figura 1: Diferentes valores del coeficiente de correlación y su correspondiente diagrama de dispersión.

Tamaño del efecto

En estadística, el tamaño del efecto es una medida de la fuerza o magnitud de un fenómeno. El coeficiente de correlación es una medida del tamaño del efecto para la relación (lineal) entre dos variables numéricas.

Se trata de un dato esencial para interpretar los resultados de nuestro estudio y su ausencia en los artículos científicos se ha identificado como uno de los 7 fallos más comunes en investigación (según la APA 19961 , 20012 ).

Para interpretar qué tan fuerte es la correlación podemos utilizar el criterio de Cohen (1988)3, quien para valores absolutos indica que valores entre:

• .1-.3 representan un efecto pequeño,
• .3-.5 un efecto medio y
• ?.5 un efecto grande.

Son valores arbitrarios que te pueden servir de guía, pero te recomiendo interpretar la fuerza (o tamaño) de la correlación según el contexto de tu investigación. No es lo mismo analizar datos de un experimento físico controlado donde habrá poco ruido en los datos, que analizar datos sociales o biológicos donde se espera encontrar menores valores de correlación debido a la gran cantidad de dispersión o variabilidad de los datos.

Cómo se mide la correlación

Veamos ahora los coeficientes de correlación más utilizados.

Tenemos el coeficiente de correlación lineal de Pearson que se sirve para cuantificar tendencias lineales, y el coeficiente de correlación de Spearman que se utiliza para tendencias de aumento o disminución, no necesariamente lineales pero sí monótonas (las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante; Figura 2).

Figura 2. Relación lineal y relación no lineal (monótona). Vemos representado con una "r" negra el coeficiente de Pearson y con una "s" en rojo el de Spearman. Cuando la relación es lineal, ambos coeficientes coinciden (valen 1), pero cuando la relación no es lineal el coeficiente de correlación de Spearman representa mejor la relación entre las variables

El coeficiente de correlación lineal de Pearson mide una tendencia lineal entre dos variables numéricas.

Es el método de correlación más utilizado, pero asume que:

• la tendencia debe ser de tipo lineal.
• no existen valores atípicos (outliers).
• las variables deben ser numé Si las variables son de tipo ordinal (como las preguntas en escala de likert), no podremos aplicar la correlación de Pearson.
• tenemos suficientes datos (algunos autores recomiendan tener más de 30 puntos u observaciones).

Los dos primeros supuestos se pueden evaluar simplemente con un diagrama de dispersión, mientras que para los últimos basta con mirar los datos y evaluar el diseño que tenemos.

El coeficiente de correlación de Spearman mide una tendencia monótona (creciente o decreciente) entre dos variables. Está basado en los rangos de los valores.

En los casos donde no se cumplen los requisitos del coeficiente de correlación lineal de Pearson, es conveniente utilizar la correlación de Spearman. Es una prueba no paramétrica (no asume una distribución previa de los datos) y es más robusta frente a la presencia de outliers que la prueba paramétrica de Pearson

Para qué sirve: ejemplos prácticos de correlación

Para calcular el coeficiente de correlación de Pearson utilizaremos la función cor() que viene instalada por defecto en los paquetes básicos de R.

Podemos ingresar las variables como vectores con cor(x, y). Recuerda, no importa cuál es “x” y cuál es “y”, porque la relación es simétrica.

Utilizaremos el conjunto de datos stackloss del paquete MASS (Brownlee, 1965) que corresponde a datos de una fábrica de oxidación de amonio (NH3) a ácido nítrico (HNO3). Son 21 observaciones de 4 variables: -   flujo del aire (representa la tasa de operación en la fábrica; AirFlow),

• temperatura del agua (WaterT emp),
• concentración de ácido (por 1000 menos 500, es decir, un valor de 89 corresponde a 58.9%; AcidConc.) y
• pérdida de ácido a través de la pila (es una medida de la ineficiencia de la planta; stack.loss).

Vamos a observar cómo se relaciona la producción de la fábrica con su eficiencia (stack.loss y Air.Flow). Como ambas son variables numéricas, vamos a estudiar su asociación mediante el coeficiente de correlación.

Primero activamos el paquete donde se encuentran los datos con la función library(), y accedemos a ellos con la función data(). Luego vemos el encabezado (las 6 primeras líneas) del conjunto de datos.

library(MASS)
data(stackloss)
head(stackloss)
## Air.Flow Water.Temp Acid.Conc. stack.loss
## 1 80 27 89 42
## 2 80 27 88 37
## 3 75 25 90 37
## 4 62 24 87 28
## 5 62 22 87 18
## 6 62 23 87 18

Podemos activar las variables con la función attach() para que sea más fácil trabajar con las variables.

attach(stackloss)
cor(x=Air.Flow, y=stack.loss)
## [1] 0.9196635

Vemos que la correlación entre ellas es positiva y fuerte r = .92. Es decir, cuando aumenta la producción de la fábrica (Air.Flow) aumenta la ineficiencia del proceso (stack.loss). O dicho de otro modo, cuando se opera en bajas cantidades en la fábrica, la ineficiencia del proceso de oxidación también es bajo.

Si tenemos más de 2 variables en una matriz o data frame (donde cada columna representa una variable distinta) utilizamos cor(x) donde “x” es una matriz o data frame.

Podemos calcular en un paso todas las correlaciones entre las variables del conjunto de datos stackloss.

cor(stackloss)
## Air.Flow Water.Temp Acid.Conc. stack.loss
## Air.Flow 1.0000000 0.7818523 0.5001429 0.9196635
## Water.Temp 0.7818523 1.0000000 0.3909395 0.8755044
## Acid.Conc. 0.5001429 0.3909395 1.0000000 0.3998296
## stack.loss 0.9196635 0.8755044 0.3998296 1.0000000

Valores ausentes

Por defecto, cuando tenemos en nuestros datos algún valor ausente o perdido (identificado en R por un “NA” de Not Available), la función cor() nos devuelve otro “NA”. Si queremos evitar este error y obtener el valor de correlación, podemos especificar cómo queremos que se traten los valores ausentes en la función mediante el argumento:

• use = ”pairwise.complete.obs”: que calcula el coeficiente de correlación para aquellas observaciones en las que no falta ningún valor de “x” ni “y”. Esto garantiza que pueda calcular la correlación para cada par de variables sin perder información debido a los valores perdidos en las otras variables.

Para calcular la correlación de Spearman en R podemos utilizar las funciones que hemos visto hasta ahora, simplemente indicando ”spearman” en el argumento method (por defecto se utiliza ”pearson”).

Si bien hemos visto que la relación entre Air.Flow y stack.loss sigue una tendencia lineal. Veamos ahora, por motivos didácticos, cómo calcularíamos el coeficiente de correlación de Spearman para el caso en que la tendencia fuera no lineal monótona.

cor(x=Air.Flow, y=stack.loss, method="spearman")
## [1] 0.9180247

Utilizamos la misma función cor() que antes pero ahora especificamos que el método sea el de Spearman.

Obtenemos un valor de correlación positivo y alto, que no varía mucho de la anterior, vale r = .92. Los valores de correlación son similares debido a que si se cumplen las condiciones de la correlación de Pearson.

Sencillo, ¿no?

En el siguiente post "Cómo evaluar si la correlación es significativa: pruebas de hipótesis para la correlación" aprenderemos a evaluar la significación de la correlación mediante pruebas de hipótesis, ¡te espero!